A Transformer based Language Model from scratch
Building transformer with simple building blocks
In this notebook i'm going to construct transformer based language model from scratch starting with the simplest building blocks. This is inspired by Chapter 12 of Deep Learning for Coders book in which it's demonstrated how to create a Recurrent Neural Network. It provides a strong intuition of how RNNs relate to regular feed-forward neural nets and why certain design choices were made. Here we aim to aquire similar kind of intuition about Transfomer based architectures.
But as always we should start with the data to be modeled, 'cause without data any model makes no particular sense.
Similar to authors of the book I'll use simple Human numbers dataset which is specifically designed to prototyping model fast and straightforward. For more details on the data one can refer to the aforemantioned book chapter which is also available for free as a notebook (isn't that awesome?!)
from fastai.text.all import *
path = untar_data(URLs.HUMAN_NUMBERS)
Path.BASE_PATH = path
path.ls()
The data consists of consecutive numbers from 1 to 9999 inclusive spelled as words.
lines = L()
with open(path/'train.txt') as f: lines += L(*f.readlines())
with open(path/'valid.txt') as f: lines += L(*f.readlines())
lines
text = ' . '.join([l.strip() for l in lines])
tokens = text.split(' ')
tokens[:10]
vocab = L(*tokens).unique()
vocab
word2idx = {w:i for i,w in enumerate(vocab)}
nums = L(word2idx[i] for i in tokens)
nums
The task will be to predict subsequent token given preceding three. This kind of tasks when the goal is to predict next token from previous ones is called autoregresive language modeling.
L((tokens[i:i+3], tokens[i+3]) for i in range(0,len(tokens)-4,3))
seqs = L((tensor(nums[i:i+3]), nums[i+3]) for i in range(0,len(nums)-4,3))
seqs
bs = 64
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], bs=64, shuffle=False)
x, y = dls.one_batch()
x.shape, y.shape
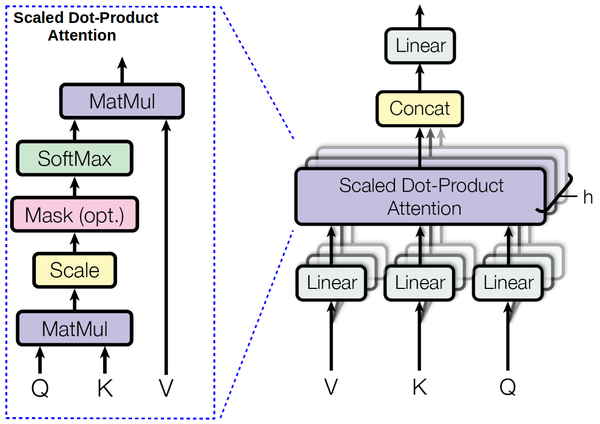
The core idea behind Transformers is Attention. Since the release of famous paper Attention is All You Need transformers has become most popular architecture for language modelling.
There are a lot of great resourses explaining transformers architecture. I'll list some of those I found useful and comprehensive:
- The Annotated Transformer completes the original paper with code
- Encoder-Decoder Model notebook by huggingface gives mathemetically grounded explanation of how transformer encoder-decoder models work
- The Illustrated GPT-2 one of the great blogposts by Jay Alammar visualizing generative language modelling on exaple of GPT-2
- minGPT cool repo by A. Karpathy providing clear minimal implementation of GPT model
There exist multiple attention mechanisms. The particular one used in the original transformer paper is Scaled Dot Product attention. Given query vector for particular token we will compare it with a key vector for each token in a sequence and decide how much value vectors of those will effect resulting representetion of the token of interest. One way to view this from a linguistic prospective is: a key is a question each word respondes to, value is information that word represent and a query is related to what every word was looking to combine with.
Mathemetically we can compute attention for all q, k, v in a matrix form:
$$\textbf {Attention}(Q,K,V) = \textbf {softmax}({QK^T\over\sqrt d_k})V $$
Note that dot product $QK^T$ results in matrix of shape (seq_len x seq_len). Then it is devided by $ \sqrt d_k$ to compensate the fact, that longer sequences will have larger dot product. $ \textbf{softmax}$ is applied to rescale the attention matrix to be betwin 0 and 1. When multiplied by $V$ it produces a matrix of the same shape as $V$ (seq_len x dv).
So where those q, k, v come from. Well that's fairly straitforward queries are culculated from the embeddings of tokens we want to find representation for by simple linear projection. Keys and values are calculated from the embeddings of context tokens. In case of self attention all of them come from the original sequence.
class SelfAttention(Module):
def __init__(self, d_in, d_qk, d_v=None):
d_v = ifnone(d_v, d_qk)
self.iq = nn.Linear(d_in, d_qk)
self.ik = nn.Linear(d_in, d_qk)
self.iv = nn.Linear(d_in, d_v)
self.out = nn.Linear(d_v, d_in)
self.scale = d_qk**-0.5
def forward(self, x):
q, k, v = self.iq(x), self.ik(x), self.iv(x)
q *= self.scale
return self.out(F.softmax(q@k.transpose(-2,-1), -1)@v)
Even though self attention mechanism is extremely useful it posseses limited expressive power. Essentially we are computing weighted some of the input modified by single affine transformation, shared across the whole sequence. To add more computational power to the model we can introduce fully connected feedforward network on top of the SelfAttention layer.
Curious reader can find detailed formal analysis of the roles of SelfAttention and FeedForward layers in transformer architecture in this paper by C. Yun et al. In brief the authors state that SelfAttention layers compute precise contextual maps and FeedForward layers then assign the results of these contextual maps to the desired output values.
class FeedForward(Module):
def __init__(self, d_in, d_ff):
self.lin1 = nn.Linear(d_in, d_ff)
self.lin2 = nn.Linear(d_ff, d_in)
self.act = nn.ReLU()
def forward(self, x):
out = self.lin2(self.act(self.lin1(x)))
return out
The output would be of shape (bs, seq_len, d) which then may be mapped to (bs, seq_len, vocab_sz) using linear layer. But we have only one target. To adress this issue we can simply do average pooling over seq_len dimention.
The resulting model is fairly simple:
class Model1(Module):
def __init__(self, vocab_sz, d_model, d_qk, d_ff):
self.emb = Embedding(vocab_sz, d_model)
self.attn = SelfAttention(d_model, d_qk)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.ff(self.attn(x))
x = x.mean(1)
return self.out(x)
model = Model1(len(vocab), 64, 64, 128)
out = model(x)
out.shape
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.lr_find()
learn.fit_one_cycle(5, 5e-3)
To evaluete the model performance we need to compare it to some baseline. Let's see what would be the accuracy if of the model which would always predict most common token.
n,counts = 0,torch.zeros(len(vocab))
for x,y in dls.valid:
n += y.shape[0]
for i in range_of(vocab): counts[i] += (y==i).long().sum()
idx = torch.argmax(counts)
idx, vocab[idx.item()], counts[idx].item()/n
As you can see, always predicting "thousand" which turn out to be the most common token in the dataset would result in ~15% accuracy. Our simple transformer does much better then that. It feels promising, so let's try to improve the architecture and check if we can get better results.
A structured sequence may comprise multiple distinctive kinds of relationships. Our model is forced to learn only one way in which queries, keys and values are constructed from the original token embedding. To remove this limitation we can modify attention layer include multiple heads which would correspond to extracting different kinds of relationships between tokens. The MultiHeadAttention layer consits of several heads each of those is similar to SelfAttention layer we made before. To keep computational cost of the multi-head layer we set $d_k = d_v = d_{model}/n_h$, where $n_h$ is number of heads.
class SelfAttention(Module):
def __init__(self, d_in, d_qk, d_v=None):
d_v = ifnone(d_v, d_qk)
self.iq = nn.Linear(d_in, d_qk)
self.ik = nn.Linear(d_in, d_qk)
self.iv = nn.Linear(d_in, d_v)
self.scale = d_qk**-0.5
def forward(self, x):
q, k, v = self.iq(x), self.ik(x), self.iv(x)
return F.softmax(q@k.transpose(-2,-1)*self.scale, -1)@v
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads, d_qk=None, d_v=None):
d_qk = ifnone(d_qk, d_model//n_heads)
d_v = ifnone(d_v, d_qk)
self.heads = nn.ModuleList([SelfAttention(d_model, d_qk) for _ in range(n_heads)])
self.out = nn.Linear(d_v*n_heads, d_model)
def forward(self, x):
out = [m(x) for m in self.heads]
return self.out(torch.cat(out, -1))
inp = torch.randn(8, 10, 64)
mha = MultiHeadAttention(64, 8)
out = mha(inp)
out.shape
class Model2(Module):
def __init__(self, vocab_sz, d_model=64, n_heads=4, d_ff=64*4):
self.emb = nn.Embedding(vocab_sz, d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.ff(self.attn(x))
x = x.mean(1)
return self.out(x)
learn = Learner(dls, Model2(len(vocab)), loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.fit_one_cycle(5, 5e-4)
Python for loops are slow, therefore it is better to refactor the MultiHeadAttention module to compute Q, K, V for all heads in batch.
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads):
assert d_model%n_heads == 0
self.n_heads = n_heads
#d_qk, d_v = d_model//n_heads, d_model//n_heads
self.iq = nn.Linear(d_model, d_model, bias=False)
self.ik = nn.Linear(d_model, d_model, bias=False)
self.iv = nn.Linear(d_model, d_model, bias=False)
self.out = nn.Linear(d_model, d_model, bias=False)
self.scale = d_model//n_heads
def forward(self, x):
bs, seq_len, d = x.size()
# (bs,sl,d) -> (bs,sl,nh,dh) -> (bs,nh,sl,dh)
q = self.iq(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
k = self.ik(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
v = self.iv(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
q*= self.scale
att = F.softmax(q@k.transpose(-2,-1), -1)
out = att @ v # (bs, nh, sl, sl) x (bs, nh, sl, dh) -> (bs, nh, sl, dh)
out = out.transpose(1, 2).contiguous().view(bs, seq_len, d) # back to original shape
return self.out(out)
learn = Learner(dls, Model2(len(vocab)), loss_func=CrossEntropyLossFlat(), metrics=accuracy)
learn.fit_one_cycle(5, 1e-3)
Note that some speedup is observed even on such a tiny dataset and small model.
Similarly to the RNN case considered in the book, we can take the next step and create more signal for the model to learn from. To adapt to the modified objective we need to make couple of steps. First let's rearrange data to proper input-target pairs for the new task.
Unlike RNN the tranformer is not a stateful model. This means it treats each sequence indepently and can only attend within fixed length context. This limitation was addressed by authors of Transformer-XL paper where adding a segment-level recurrence mechanism and a novel positional encoding scheme were proposed to enable capturing long-term dependencies. I will not go into details of TransformerXL architecture here. As we shell see stateless transformer can also learn a lot about the structure of our data.
One thing to note in this case is that we don't need to maintain the structure of the data outside of the sequences, so we can shuffle the sequences randomly in the dataloader.
sl = 16
seqs = L((tensor(nums[i:i+sl]), tensor(nums[i+1:i+sl+1]))
for i in range(0,len(nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:],
bs=bs, drop_last=True, shuffle=True)
xb, yb = dls.one_batch()
xb.shape, yb.shape
[L(vocab[o] for o in s) for s in seqs[0]]
Before we did average pooling over seq_len dimension. Our model didn't care about the order of the tokens at all. But actually order of the tokens in a sentence matter a lot. In our case one hundred two and two hundred one are pretty different and hundred one two doesn't make sense.
To encorporate positional information into the model authors of the transformer architecture proposed to use positional encodings in addition to regular token embeddings. Positional encodings may be learned, but it's also possible to use hardcoded encodings. For instance encodings may be composed of sin and cos. In this way each position in a sequence will get unique vector associated with it.
class PositionalEncoding(Module):
def __init__(self, d):
self.register_buffer('freq', 1/(10000 ** (torch.arange(0., d, 2.)/d)))
self.scale = d**0.5
def forward(self, x):
device = x.device
pos_enc = torch.cat([torch.sin(torch.outer(torch.arange(x.size(1), device=device), self.freq)),
torch.cos(torch.outer(torch.arange(x.size(1), device=device), self.freq))],
axis=-1)
return x*self.scale + pos_enc
x = torch.zeros(1, 16, 64)
encs = PositionalEncoding(64)(x)
plt.matshow(encs.squeeze())
plt.xlabel('Embedding size')
plt.ylabel('Sequence length')
plt.show()
class TransformerEmbedding(Module):
def __init__(self, emb_sz, d_model):
self.emb = nn.Embedding(emb_sz, d_model)
self.pos_enc = PositionalEncoding(d_model)
def forward(self, x):
return self.pos_enc(self.emb(x))
class Model3(Module):
def __init__(self, vocab_sz, d_model=64, n_heads=4, d_ff=64*4):
self.emb = TransformerEmbedding(vocab_sz, d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.ff(self.attn(x))
return self.out(x)
model = Model3(len(vocab))
out = model(xb)
out.shape
def loss_func(inp, targ):
return F.cross_entropy(inp.view(-1, len(vocab)), targ.view(-1))
learn = Learner(dls, Model3(len(vocab)), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(5, 1e-2)
Wow! That's a great accuracy! So the problem is solved and we only needed one attention layer and 2 layer deep feed-forward block? Don't you feel somewhat skeptical about this result?
Well, you should be! Think about what we did here: the goal was to predict a target sequence, say ['.','two','.','three','.','four'] from an input ['one','.','two','.','three','.']. These two sequences intersect on all positions except the first and the last one. So models needs to learn simply to copy input tokens starting from the second one to the outputs. In our case this will result in 15 correct predictions of total 16 positions, that's almost 94% accuracy. This makes the task very simple but not very useful to learn. To train proper autoregressive language model, as we did with RNNs, a concept of masking is to be introduced.
So we want to allow the model for each token to attend only to itself and those prior to it. To acomplish this we can set all the values of attention matrix above the main diagonal to $-\infty$. After softmax this values will effectively turn to 0 thus disabling attention to the "future".
def get_subsequent_mask(x):
sz = x.size(1)
mask = (torch.triu(torch.ones(sz, sz, device=x.device)) == 1).transpose(0, 1)
mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
return mask
inp = torch.randn(8, 10, 64)
mask = get_subsequent_mask(inp)
plt.matshow(mask);
q, k = torch.rand(1,10,32), torch.randn(1,10,32)
att_ = F.softmax((q@k.permute(0,2,1)+mask), -1)
plt.matshow(att_[0].detach());
We should also modify the attention layer to accept mask:
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads):
assert d_model%n_heads == 0
self.n_heads = n_heads
d_qk, d_v = d_model//n_heads, d_model//n_heads
self.iq = nn.Linear(d_model, d_model, bias=False)
self.ik = nn.Linear(d_model, d_model, bias=False)
self.iv = nn.Linear(d_model, d_model, bias=False)
self.scale = d_qk**-0.5
self.out = nn.Linear(d_model, d_model, bias=False)
def forward(self, x, mask=None):
bs, seq_len, d = x.size()
mask = ifnone(mask, 0)
q = self.iq(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
k = self.ik(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
v = self.iv(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
q*= self.scale
att = F.softmax(q@k.transpose(-2,-1) + mask, -1)
out = att @ v # (bs, nh, sl, sl) x (bs, nh, sl, dh) -> (bs, nh, sl, dh)
out = out.transpose(1, 2).contiguous().view(bs, seq_len, d) # back to original shape
return self.out(out)
class Model4(Module):
def __init__(self, vocab_sz, d_model=64, n_heads=8, d_ff=64*4):
self.emb = TransformerEmbedding(vocab_sz, d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
mask = get_subsequent_mask(x)
x = self.ff(self.attn(x, mask))
return self.out(x)
learn = Learner(dls, Model4(len(vocab)), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(5, 3e-3)
Now we get somewhat lower accuracy, which is expected given that the task has become more difficult. Also training loss is significantly lower than validation loss, which means the model is overfitting. Let's see if the same approaches as was applied to RNNs can help.
To solve a more difficult task we ussualy need a deeper model. For convenience let's make a TransformerLayer which will combine self-attention and feed-forward blocks.
class TransformerLayer(Module):
def __init__(self, d_model, n_heads=8, d_ff=None, causal=True):
d_ff = ifnone(d_ff, 4*d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff)
self.causal = causal
def forward(self, x, mask=None):
if self.causal:
mask = get_subsequent_mask(x)
return self.ff(self.attn(x, mask))
class Model5(Module):
def __init__(self, vocab_sz, d_model=64, n_layer=4, n_heads=8):
self.emb = TransformerEmbedding(vocab_sz, d_model)
self.encoder = nn.Sequential(*[TransformerLayer(d_model, n_heads) for _ in range(n_layer)])
self.out = nn.Linear(d_model, vocab_sz)
def forward(self, x):
x = self.emb(x)
x = self.encoder(x)
return self.out(x)
learn = Learner(dls, Model5(len(vocab), n_layer=4), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(5, 1e-2)
That's not good! 4 layer deep Transformer strugles to learn anything. But there are good news, this problem has been already resolved in the original transformer.
If you are familiar with ResNets the proposed solution will not surprise you much. The idea is simple yet very effective. Instead of returning modified output $f(x)$ each transformer sublayer will return $x + f(x)$. This allows the original input to propagate freely through the model. So the model learns not an entirely new representation of $x$ but how to modify $x$ to add some useful information to the original representation.
As we modify layers to include the residual connections let's also add some regularization by inserting Dropout layers.
class TransformerEmbedding(Module):
def __init__(self, emb_sz, d_model, p=0.1):
self.emb = Embedding(emb_sz, d_model)
nn.init.trunc_normal_(self.emb.weight, std=d_model**-0.5)
self.pos_enc = PositionalEncoding(d_model)
self.drop = nn.Dropout(p)
def forward(self, x):
return self.drop(self.pos_enc(self.emb(x)))
Another modification is to add layer normalization which is intended to improve learning dynamics of the network by reparametrising data statistics and is generally used in transformer based architectures.
class FeedForward(Module):
def __init__(self, d_model, d_ff, p=0.2):
self.lin1 = nn.Linear(d_model, d_ff)
self.lin2 = nn.Linear(d_ff, d_model)
self.act = nn.ReLU()
self.norm = nn.LayerNorm(d_model)
self.drop = nn.Dropout(p)
def forward(self, x):
x = self.norm(x)
out = self.act(self.lin1(x))
out = self.lin2(out)
return x + self.drop(out)
class MultiHeadAttention(Module):
def __init__(self, d_model, n_heads, p=0.1):
assert d_model%n_heads == 0
self.n_heads = n_heads
d_qk, d_v = d_model//n_heads, d_model//n_heads
self.iq = nn.Linear(d_model, d_model, bias=False)
self.ik = nn.Linear(d_model, d_model, bias=False)
self.iv = nn.Linear(d_model, d_model, bias=False)
self.scale = d_qk**0.5
self.out = nn.Linear(d_model, d_model, bias=False)
self.norm = nn.LayerNorm(d_model)
self.drop = nn.Dropout(p)
def forward(self, x, mask=None):
bs, seq_len, d = x.size()
mask = ifnone(mask, 0)
x = self.norm(x)
k = self.ik(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
q = self.iq(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
v = self.iv(x).view(bs, seq_len, self.n_heads, d//self.n_heads).transpose(1, 2)
att = F.softmax(q@k.transpose(-2,-1)/self.scale + mask, -1)
out = att @ v # (bs, nh, sl, sl) x (bs, nh, sl, dh) -> (bs, nh, sl, dh)
out = out.transpose(1, 2).contiguous().view(bs, seq_len, d) # back to original shape
return x + self.drop(self.out(out))
class TransformerLayer(Module):
def __init__(self, d_model, n_heads=8, d_ff=None, causal=True,
p_att=0.1, p_ff=0.1):
d_ff = ifnone(d_ff, 4*d_model)
self.attn = MultiHeadAttention(d_model, n_heads)
self.ff = FeedForward(d_model, d_ff, p=p_ff)
self.causal = causal
self._init()
def forward(self, x, mask=None):
if self.causal:
mask = get_subsequent_mask(x)
return self.ff(self.attn(x, mask))
def _init(self):
for p in self.parameters():
if p.dim()>1: nn.init.xavier_uniform_(p)
class Model6(Module):
def __init__(self, vocab_sz, d_model=64, n_layer=4, n_heads=8,
p_emb=0.1, p_att=0.1, p_ff=0.2, tie_weights=True):
self.emb = TransformerEmbedding(vocab_sz, d_model, p=p_emb)
self.encoder = nn.Sequential(*[TransformerLayer(d_model, n_heads,
p_att=p_att, p_ff=p_ff)
for _ in range(n_layer)],
nn.LayerNorm(d_model))
self.out = nn.Linear(d_model, vocab_sz)
if tie_weights: self.out.weight = self.emb.emb.weight
def forward(self, x):
x = self.emb(x)
x = self.encoder(x)
return self.out(x)
learn = Learner(dls, Model6(len(vocab), n_layer=2), loss_func=loss_func, metrics=accuracy)
learn.fit_one_cycle(8, 1e-2)
Learning to predict numbers is great, but let's try something more entertaining. We can train a language model to generate texts. For example let's try to generate some text in style of Lewis Carroll. For this we'll fit a language model on "Alice in Wonderland" and "Through the looking glass".
def parse_txt(fns):
txts = []
for fn in fns:
with open(fn) as f:
tmp = ''
for line in f.readlines():
line = line.strip('\n')
if line:
tmp += ' ' + line
elif tmp:
txts.append(tmp.strip())
tmp = ''
return txts
texts = parse_txt([path/'11-0.txt', path/'12-0.txt'])
len(texts)
texts[0:2]
class CharTokenizer(Transform):
"Simple charecter level tokenizer"
def __init__(self, vocab=None):
self.vocab = ifnone(vocab, ['', 'xxbos', 'xxeos'] + list(string.printable))
self.c2i = defaultdict(int, [(c,i) for i, c in enumerate(self.vocab)])
def encodes(self, s, add_bos=False, add_eos=False):
strt = [self.c2i['xxbos']] if add_bos else []
end = [self.c2i['xxeos']] if add_eos else []
return LMTensorText(strt + [self.c2i[c] for c in s] + end)
def decodes(self, s, remove_special=False):
return TitledStr(''.join([self.decode_one(i) for i in s]))
def decode_one(self, i):
if i == 2: return '\n'
elif i == 1: return ''
else: return self.vocab[i]
@property
def vocab_sz(self):
return len(self.vocab)
tok = CharTokenizer()
def add_bos_eos(x:list, bos_id=1, eos_id=2):
return [bos_id] + x + [eos_id]
nums = [add_bos_eos(tok(t.lower()).tolist()) for t in texts]
len(nums)
all_nums = []
for n in nums: all_nums.extend(n)
all_nums[:15]
print(tok.decode(all_nums[:100]))
sl = 512
seqs = L((tensor(all_nums[i:i+sl]), tensor(all_nums[i+1:i+sl+1]))
for i in range(0,len(all_nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], device='cuda',
bs=8, drop_last=True, shuffle=True)
xb, yb = dls.one_batch()
xb.shape, yb.shape
model = Model6(tok.vocab_sz, 512, 6, p_emb=0.1, p_ff=0.1, tie_weights=True)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=[accuracy, perplexity]).to_native_fp16()
learn.lr_find()
learn.fit_one_cycle(50, 5e-4, cbs=EarlyStoppingCallback(patience=5))
Text generation
Text generation is a big topic on it's own. One can refer to great posts by Patrick von Platen from HuggingFace and Lilian Weng for more details on various approaches. Here I will use nucleus sampling. This method rallies on sampling from candidates compounding certain value of probability mass. Intuitively this approach should work for character level generation: when there is only one grammatically correct option for continuation we always want to select it, but when starting a new word some diversity in outputs is desirable.
def expand_dim1(x):
if len(x.shape) == 1:
return x[None, :]
else: return x
def top_p_filter(logits, top_p=0.9):
sorted_logits, sorted_indices = torch.sort(logits, descending=True)
cum_probs = torch.cumsum(F.softmax(sorted_logits, dim=-1), dim=-1)
sorted_indices_to_remove = cum_probs > top_p
sorted_indices_to_remove[..., 1:] = sorted_indices_to_remove[..., :-1].clone()
sorted_indices_to_remove[..., 0] = 0
indices_to_remove = sorted_indices_to_remove.scatter(1, sorted_indices, sorted_indices_to_remove)
logits[indices_to_remove] = float('-inf')
return logits
@torch.no_grad()
def generate(model, inp,
max_len=50,
temperature=1.,
top_k = 20,
top_p = 0.9,
early_stopping=False, #need eos_idx to work
eos_idx=None):
model.to(inp.device)
model.eval()
thresh = top_p
inp = expand_dim1(inp)
b, t = inp.shape
out = inp
for _ in range(max_len):
x = out
logits = model(x)[:, -1, :]
filtered_logits = top_p_filter(logits)
probs = F.softmax(filtered_logits / temperature, dim=-1)
sample = torch.multinomial(probs, 1)
out = torch.cat((out, sample), dim=-1)
if early_stopping and (sample == eos_idx).all():
break
return out
out = generate(learn.model, tok('Alice said '), max_len=200, early_stopping=True, eos_idx=tok.c2i['xxeos'])
print(tok.decode(out[0]))
Our relatively simple model learned to generate mostly grammatically plausible text, but it's not entirely coherent. But it would be too much to ask from the model to learn language from scratch by "reading" only two novels (however great those novels are). To get more from the model let's feed it larger corpus of data.
For this purpose I will use a sample from bookcorpus dataset.
dataset = load_dataset("bookcorpus", split='train')
df = pd.DataFrame(dataset[:10_000_000])
df.head()
df['len'] = df['text'].str.len()
cut = int(len(df)*0.8)
splits = range_of(df)[:cut], range_of(df[cut:])
tfms = Pipeline([ColReader('text'), tok])
dsets = Datasets(df, tfms=tfms, dl_type=LMDataLoader, splits=splits)
@patch
def create_item(self:LMDataLoader, seq):
if seq>=self.n: raise IndexError
sl = self.last_len if seq//self.bs==self.n_batches-1 else self.seq_len
st = (seq%self.bs)*self.bl + (seq//self.bs)*self.seq_len
txt = self.chunks[st : st+sl+1]
return LMTensorText(txt[:-1]),txt[1:]
%%time
dl_kwargs = [{'lens':df['len'].values[splits[0]]}, {'val_lens':df['len'].values[splits[1]]}]
dls = dsets.dataloaders(bs=32, seq_len=512, dl_kwargs=dl_kwargs, shuffle_train=True, num_workers=2)
dls.show_batch(max_n=2)
model = Model6(tok.vocab_sz, 512, 8, p_emb=0.1, p_ff=0.1, tie_weights=True)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=[accuracy, perplexity]).to_native_fp16()
learn.lr_find()
learn = learn.load(path/'char_bookcorpus_10m')
learn.fit_one_cycle(1, 1e-4)
learn.save(path/'char_bookcorpus_10m')
sl = 512
seqs = L((tensor(all_nums[i:i+sl]), tensor(all_nums[i+1:i+sl+1]))
for i in range(0,len(all_nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], device='cuda',
bs=16, drop_last=True, shuffle=True)
model = Model6(tok.vocab_sz, 512, 8, p_emb=0.1, p_ff=0.1, tie_weights=True)
learn = Learner(dls, model, loss_func=CrossEntropyLossFlat(), metrics=[accuracy, perplexity]).to_native_fp16()
learn = learn.load(path/'char_bookcorpus_10m')
learn.lr_find()
learn.fit_one_cycle(10, 1e-4)
As you see pretraining model on large corpus followed by finetuning helped to reduce validation loss from arount 1.53 to 1.037 and improve accuracy in predicting next character to 68% (compared to 56.7% before). Let's see how it effects sampled text:
out = generate(learn.model, tok('Alice said '), max_len=200, early_stopping=True, eos_idx=tok.c2i['xxeos'])
print(tok.decode(out[0]))